Statistik für Pflegeberufe
- Add new comment
- 25073 reads

Image by Bob.Fornal via Flickr
Statistik für Pflegeberufe
Ein kleiner Kurs
Auch wenn man es zunächst vielleicht nicht erwartet, so hat Statistik doch eine wichtige Bedeutung für die wissenschaftliche Herangehensweise an die Pflege gewonnen. Auf diesen Seiten entsteht daher ein kleiner Kurs, der parallel zu meinen Vorlesungen "Statistik" im Bachelor-Studiengang Pflege an der FH Frankfurt im Sommersemester 2009 geschrieben wird.
Diese Webseiten sollen als interaktives Skript dienen. Eingearbeitete Links und Tests werden der Vertiefung und Festigung der Inhalte dienen. Diese Seiten sind primär für meine Studierenden gedacht, aber ich freue mich über jeden, der für sich einen Nutzen daraus ziehen kann.
Wichtigstes Lernziel
Dieser Kurs soll dazu beitragen, dass Sie mit statistischen Grundbegriffen vertraut werden, damit Sie zukünftig besser in der Lage sind, wissenschaftliche Artikel in denen Standardverfahren der Statistik angewandt werden, lesen und beurteilen können. Sie sollen kein Statistiker werden - Sie sollen aber die Sprache der Statistik in Grundzügen verstehen können. Dann werden Sie feststellen, dass auch hier nur mit Wasser gekocht wird, und manches viel einfacher ist, als Sie vorher dachten.
Zielgruppe
Dieser Kurs ist offen für alle Interessierten und kann unabhängig von der Vorlesung genutzt werden.
Was müssen Sie ein - und mitbringen?
Sie brauchen keine tiefergehenden mathematischen Kenntnisse. Manche von Ihnen haben vielleicht sogar Mathematik in der Schule abgewählt und sind überrascht, dass sie gerade in diesem Zusammenhang wieder damit konfrontiert werden. Ich werde versuchen, die Mathematik so einfach wie möglich zu halten.
Sie brauchen aber Ausdauer. Die Denkweise der Statistik ist zunächst ungewohnt für Sie. Lassen Sie sich nicht entmutigen. Betrachten Sie das ganze wie einen Besuch im Fitness-Studio, und Sie werden Regionen Ihres Gehirns entdecken, von denen Sie gar nicht wussten, das sie existieren.
Für die Studierenden meiner Vorlesung ist wichtig: Sie müssen die Inhalte der Vorlesung nacharbeiten und vertiefen, da die Inhalte der einzelnen Vorlesungen aufeinander aufbauen. Um diese verstehen zu können, sollten Sie mit vorangegangenen Inhalten vertraut sein. Ansonsten verlieren Sie sehr leicht den Anschluss! D.h. diese Vorlesung erfordert kontinuierliches Mitarbeiten.
Es geht im wesentlichen darum, eine neue Sprache, die Sprache der Statistik zu erlernen. Das erfordert Zeit und Aufwand. Ich werde Ihnen dabei helfen.
Was Sie ebenfalls benötigen, sind grundlegende Kenntnisse der englischen Sprache. Die meiste wissenschaftliche Literatur zu Themen der Pflege ist in Englisch. Üben Sie diese Sprache, ansonsten geht es Ihnen wie dem Kunden im Supermarkt, der sich nicht traut, an der Käsetheke zu bestellen, da er die Namen der einzelnen Käsesorten nicht kennt. Ihm entgeht eine ganze Welt des Geschmacks.
Achtung
Dieser Kurs lebt! Er wird in diesem Semester hier erst nach und nach aufgebaut. Die Webseiten können sich daher täglich verändern. Daher werden sich sicher auch Fehler auf den Seiten finden lassen. Daher ...
Wichtig
Ich kann es nicht oft genug betonen und werde an vielen Stellen darauf hinweisen: Wie gut dieser Kurs wird, hängt auch von Ihnen ab. Nutzen Sie die Möglichkeit zum Kommentieren, die sich unten auf jeder Seite befindet, um mich auf Fehler aufmerksam zu machen, oder um mir Hinweise zu geben, wie Ihnen der Kurs noch mehr Nutzen bringen kann. Darüber hinaus können hier auch interessante Themen diskutiert werden. Trauen Sie sich! Natürlich brauchen Sie nicht Ihren Namen zu nennen.
tags:
Language:
Quizmaster oder die Folterkammer
- 17995 reads
|
Wählen Sie sich einen Quiz aus, und testen Sie Ihr Wissen. Sie können das beliebig häufig wiederholen. Es werden aus einem Pool von Fragen jeweils zufällig neue Fragen herausgesucht, so dass der Quiz immer etwas anders ausfallen sollte. |
- Quiz: Umgang mit Risiken
- Quiz: Grundbegriffe
- Quiz: Kennzahlen
- Quiz: Kennzahlen und Darstellungen für unterschiedlich skalierte Merkmale
- Quiz: Zentraler Grenzwertsatz und Normalverteilung
- Quiz: Statistisches Schätzen
- Quiz: Statistisches Testen
- Quiz: All together now ...
Es kommen weitere Quizze (?) hinzu, und es werden laufend neue Fragen aufgenommen.
tags:
Language:
Wie gehe ich mit dem Kurs um?
- Add new comment
- 9125 reads

Image by mac steve via Flickr
Wie gehe ich mit dem Kurs um?
Diese Webseiten entwickle ich als Begleitung für meine Vorlesung "Statistik" im Bachelor-Studiengang Pflege der FH Frankfurt. Sie sollen als interaktives Skript dienen. Eingearbeitete Links und Tests werden der Vertiefung und Festigung der Inhalte dienen. Obwohl diese Seiten für meine Studierenden gedacht sind, freue ich mich über jeden, der für sich einen Nutzen daraus ziehen kann.
Diese Webseiten werden im Verlauf des Sommersemesters 2009 entstehen. Es gilt folgende Spielregel für die Nutzung:
Spielregel: Wenn Ihnen fehlerhafte Inhalte auffallen, Sie sich etwa auf den Seiten wünschen oder einfach Fragen, Hinweise, Tipps oder Kritik loswerden wollen, dann schreiben Sie einen Kommentar. Sie haben auf jeder Seite unten die Möglichkeit auch anonym diesen zu verfassen. Nur durch diese Hinweise kann ich das Angebot verbessern. Vielen Dank!
Aufbau der einzelnen Seiten
Jede Seite befasst sich mit einem Themenkomplex. Sie besteht aus den folgenden Teilen:
- Was sollten Sie schon wissen?
- Was sollten Sie erledigt haben?
- Knappe Vorstellung des Themas. Diese Seiten sollen kein Lehrbuch ersetzen. Es gibt bereits eine Vielzahl guter Lehrbücher. Siehe Literaturverzeichnis.
- Links zu Ressourcen zu diesem Thema.
- Schlammloch
Diese Aufgabe wird zu jedem Thema gestellt. Schildern Sie ganz kurz (max. 250 Zeichen), was Ihnen bei diesem Thema am unklarsten ist. Sie können diese Angabe anonym machen. - Selbstkontrolle
Dies ist ein knapper Multiple-Choice-Test in dem wichtige Aspekte noch einmal abgefragt werden. Diesen Test können Sie beliebig häufig wiederholen und auch er ist natürlich anonym. - Der Möglichkeit die Seite zu kommentieren.
tags:
Language:
Übersicht über die Lektionen
- Add new comment
- 9510 reads
Übersicht über die Lektionen
kommt noch
tags:
Language:
Lektion 1: Umgang mit Risiken und Wahrscheinlichkeiten
- Add new comment
- 9484 reads
| Attachment | Size |
|---|---|
| 169.1 KB | |
| 184.58 KB |
Wahrscheinlichkeiten und Risiken begegnen uns überall im Alltag. Die Frage, ob eine Ampel bei Rot überquert werden soll, ist nichts anderes als ein Abwägen von Risiken. Das Stellen einer Pflegediagnose ist die Suche nach derjenigen Pflegediagnose, die mit der höchsten Wahrscheinlichkeit, die bei einem Patienten beobachteten Symptome erklärt. Die Entscheidung für einer Pflegetätigkeit ist die Suche nach der Maßnahme, die eine ausreichend hohe Wahrscheinlichkeit auf Besserung für den Patienten mit sich bringt. Ebenso ist die Abwägung, ob ein diagnostischer Eingriff durchgeführt werden soll, der wiederum mit bestimmten Risiken verbunden ist, primär ein Problem der Bestimmung von Wahrscheinlichkeiten. Die informierte Zustimmung eines Patienten zu einem solchen Eingriff erfordert Grundkenntnisse des Umgangs mit Risiken beim Diagnostiker und Therapeuten sowie dem Patienten selber
Die in dieser Veranstaltung vorgestellten Überlegungen und Beispiele basieren auf dem hervorragenden und unterhaltsam zu lesendem Buch von Gigerenzer
Die Folien zur Vorlesung
Download der aktuellen Folien unten auf der Seite.
Mehr dazu
20 Minuten mit Peter Donnely: How Juries are fooled by statistics.
Noch mehr dazu
Youtube (4:35 Minuten/deutsch): Brustkrebsvorsorge nützlich? Bericht über die Ergebnisse der Arbeiten von Gigerenzer.
Interaktive Übung
In dieser interaktiven Übung werden die verschiedenen Begriffe noch einmal in Beziehung gesetzt. Probieren Sie die verschiedenen Darstellung ein und desselben Sachverhaltes aus.
Welche Darstellung ist am meisten informativ?
Weitere Animationen und mehr Infos
Vorlesungsaufzeichnung
Aufgaben
- Erproben Sie die neuen Begriffe in der interaktiven Übung auf dieser Seite.
- Machen Sie Ihren Eintrag im Statistik-Schlammloch weiter unten.
- Füllen Sie den Fragebogen aus. Wir benötigen die Daten für die folgenden Veranstaltungen.
-
Sehen Sie sich den Artikel aus Zeit-Online an. Ein schönes Beispiel aus der Kriminalistik, das vieles relativiert.
Dem Täter auf der Spur!
tags:
Language:
Quiz: Diagnostisches Testen
- 12586 reads
In diesem Test werden Ihre Kenntnisse über Sensitivität, Spezifität und die prädiktiven Werte überprüft.
Lektion 2: Grundbegriffe
- Add new comment
- 30331 reads
| Attachment | Size |
|---|---|
| 124.64 KB |
Was sollten Sie bis hierhin kennen?
- Sie sollten die neuen Begriffe: Sensitivität, Spezifität, Prädiktiver Wert eines positiven Testergebnisses, Prädiktiver Wert eines negativen Testergebnisses unterscheiden können.
- Sie sollten wissen, warum die Prävalenz für der Bestimmung der prädiktiven Werte positiver und negativer Testergebnisse wichtig ist, und welche Folgen sich daraus ergeben.
- Sie sollten die verschiedenen Begriffe wie relative Risikoreduktion, absolute Risikoreduktion, Anzahl der notwendigen Behandlungen unterscheiden können.
- Sie sollten die Problematik von Screening-Maßnahmen schildern können.
Was sollten Sie bis jetzt erledigt haben?
- Sie sollten die einleitenden Seiten dieser Statistik-Website gelesen haben.
- Sie sollten die neuen risikobezogenen Begriffe in der interaktiven Übung in Lektion 1 kennengelernt haben und sich mit den zugehörigen englischen Begriffen vertraut gemacht haben.
- Sie sollten Ihren Eintrag im Statistik-Schlammloch für Lektion 1 erledigt haben.
- Der Fragebogen sollte ausgefüllt sein.
Grundbegriffe
Grundgesamtheit - Stichprobe
Oft interessiert einen generalisierte Aussagen über etwa das Dekubitusrisiko aller Diabetes-Patienten zu machen. Diese stellen dann die sogenannte Grundgesamtheit dar. Aus praktischen Überlegungen heraus kann man in der Regel allerdings nie alle Beobachtungseinheiten der Grundgesamtheit untersuchen, sondern man muss sich auf eine Teilmenge, eine Stichprobe beschränken.
Beobachtungseinheit - Merkmalsträger
Das einzelne Objekt der Untersuchung oder Studie wird als Beobachtungseinheit oder Merkmalsträger bezeichnet. Aufgabe der Untersuchung ist es festgelegte Merkmale dieser Beobachtungseinheit zu messen oder zu bestimmen.
Merkmal (Variable)
Ein Merkmal (Eine Variable) ist eine Eigenschaft einer Beobachtungseinheit, die gemessen oder anderweitig bestimmt werden kann. Merkmale können etwa bestimme Symptome oder einzelne Vitalparameter sein.
Merkmalsausprägung
Die Werte, die ein Merkmal annehmen kann, werden als Merkmalsausprägungen bezeichnet. Merkmalsausprägungen können etwa die Gradeinteilungen eines Dekubitus sein, wenn das Merkmal "Schweregrad des Dekubitus" ist.
Qualitativ – Quantitativ
Es wird zwischen qualitativen und quantitativen Merkmalen unterschieden. Qualitative Merkmale sind Merkmale, die sich nicht durch Zahlen direkt erfassen lassen. Beispiele wären etwa eine Blutgruppe, Haarfarbe, Beruf und Ausbildung.
Quantitative Merkmale sind dagegen durch Zahlen bestimmbar. Diese Merkmale lassen sich durch wiegen, messen, abzählen usw. bestimmen.
Nominal – Ordinal
Qualitive Merkmale bei denen eine Rangfolge der Merkmalsausprägungen festgelegt werden kann, werden als ordinale Merkmale bezeichnet. Ein Beispiel für ein ordinales Merkmals wäre etwa das Merkmal „größter Ausbildungsabschluss“. Die Merkmalsausprägungen „Hauptschulabschluss“, „Realschulabschluss“, „Gymnasialabschluss“, „Hochschulabschluss“ lassen sich in eine Rangfolge bringen. Ein sinnvoller Abstand zwischen den einzelnen Merkmalsausprägungen lässt sich aber nicht bestimmen. Ist eine solche Rangfolge nicht sinnvoll möglich, so wird von einem nominalen Merkmal gesprochen.
Diskret - Stetig
Quantitative Merkmale werden dabei weiter in quantitativ diskrete und quantitativ stetige Merkmale unterschieden. Diskrete Merkmale können nur bestimmte Werte annehmen. So kann das diskrete Merkmal Kinderzahl nur ganze positive Zahlen annehmen. Im Gegensatz dazu kann die Körpergröße in einem bestimmten sinnvollen Bereich jeden beliebigen Wert annehmen. Die Körpergröße ist ein stetiges Merkmal.
Die Unterscheidung der Merkmale in quantitative und qualitative, ordinale und nominale Merkmale ist wichtig, da hierdurch bestimmt wird, welche statistischen Methoden angewandt werden dürfen.
Vorlesungsaufzeichnung
Beschreibende Statistik
Die Aufgabe der beschreibenden Statistik ist ganz einfach. Stellen Sie sich vor, Sie haben ein bestimmtes Merkmal, bsp. den Kopfumfang bei 1500 Neugeborenen gemessen. Sie sind fertig und werden von einem Bekannten angerufen. Dieser fragt sie, was denn bei der Studie herausgekommen ist. Sie können jetzt ja schlecht die 1500 Messergebnisse vorlesen. Aufgabe der beschreibenden Statistik ist es, diese so aufzubereiten, dass wichtige Aspekte in Kennzahlen zusammengefasst werden, oder aber mit graphischen Methoden visualisiert werden. In der folgenden Lektion geht es um die Kennzahlen der beschreibenden Statistik.
Image by Tjflex2 via Flickr
tags:
Language:
Quiz: Grundbegriffe
- 13062 reads
Überprüfen Sie Ihr Wissen über Grundbegriffe der Statistik.
Lektion 3: Kennzahlen der beschreibenden Statistik
- Add new comment
- 10672 reads
| Attachment | Size |
|---|---|
| 111.17 KB |
Zunächst werden quantitative Merkmale betrachtet. Die wichtigsten Kennzahlen hierbei können in zwei Kategorien unterschieden werden.
-
Lagemaße
Die Lagemaße geben an, wo sich die beobachteten Werte befunden haben. Wichtig dabei sind der kleinste und größte Wert sowie die Angabe der Mitte der Werte. -
Streuungsmaße
Die Streuungmaße wiederum liefern Hinweise darauf, wie dicht die Werte beeinander gelegen haben, oder wie stark sie (um die Mitte) streuen.
Die n beobachteten Werte des quantitativen Merkmals X werden kurz als
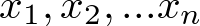
bezeichnet.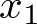 ist dabei der 1. beobachtete Wert,
ist dabei der 1. beobachtete Wert, 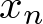 der letzte beobachtete Wert.
der letzte beobachtete Wert.
Lagemaße - Lokalisationsmaße
Die Lagemaße liefern Kennzahlen, die beschreiben, wo die beobachteten Werte liegen. Allgemein werden die beobachteten Werte häufig beschrieben:
-
Minimum - der kleinste beobachtete Wert
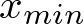
-
Maximum - der größte beobachtete Wert
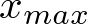
-
Modalwert(e) - der Wert, der am häufigsten beobachtet wurde. Falls mehrere Werte gleichhäufig am meisten beobachtet wurden, so kann es auch mehrere Modalwerte geben. (Eselsbrücke: Der Wert, der in Mode ist.)
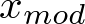
-
Das arithmetische Mittel - Mittelwert - Durchschnitt
Ist ein Maß für den Schwerpunkt der Werte.
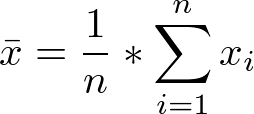
(Es werden alle beobachteten Werte aufaddiert. Die Summe wird durch die Anzahl der beobachteten Werte geteilt.). Das arithmetische Mittel hat den Nachteil, dass alle Werte, und damit auch sehr extreme Werte bei der Bestimmung der Mitte berücksichtigt werden. Dieses kann manchmal die Aussagekraft beeinträchtigen. Daher wird noch ein weiteres Maß für die Mitte verwendet. -
Der Median - Der Wert, bei dem mindestens die Hälfte der beobachteten Werte kleiner oder gleich sind. Seien nun

die der Größe nach angeordneten Beobachtungen
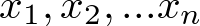
Bei der Bestimmung des Medians sind zwei Fälle zu unterscheiden:
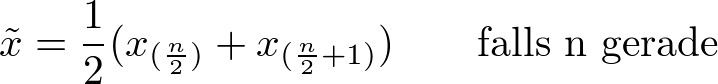
und

Streuungsmaße - Dispersionsmaße
-
Die Spannweite - Die Breite des Intervalls in dem alle beobachteten Werte zu finden sind.
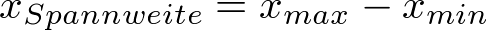
-
Die empirische Varianz
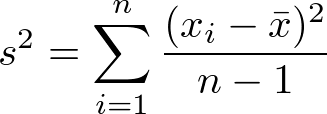
-
Die empirische Standardabweichung
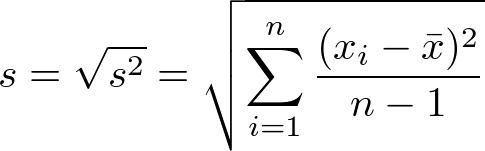
Vorlesungsaufzeichnung
Aufgaben
Der Fragebogen "Einstellung zur Statistik" wurde von 14 Personen beantwortet. Es wurden die folgenden Angaben bezüglich der Merkmale Alter und "Wie lange liegt der Mathematikuntericht zurück" gemacht.
| Nr. | Alter | Jahre seit Matheunterricht |
| 1 | 25 | 5 |
| 2 | 29 | 10 |
| 3 | 21 | 2 |
| 4 | 22 | 3 |
| 5 | 26 | 4 |
| 6 | 27 | 8 |
| 7 | 26 | 9 |
| 8 | 43 | 25 |
| 8 | 23 | 4 |
| 10 | 22 | 3 |
| 11 | 31 | 12 |
| 12 | 22 | 2 |
| 13 | 46 | 27 |
| 14 | 22 | 3 |
Beschreiben Sie die Beobachtungen durch geeignete Kenngrößen!
Selbstkontrolle

Image by Juergen Kurlvink via Flickr
tags:
Language:
Quiz: Kennzahlen
- 11236 reads
Hier können Sie Ihre Kenntnisse der statistischen Kennzahlen überprüfen.
Lektion 4: Graphische Darstellung
- Add new comment
- 10601 reads
| Attachment | Size |
|---|---|
| 1019.94 KB |
Neben der Angabe der Kennzahlen ist die graphische Darstellung ein wichtiges Verfahren zur Kommunikation der der vorgefundenen Ergebnisse in einer Stichprobe. Ein Bild sagt mehr als tausend Worte.
(Klicken Sie auf die Abbildungen, um diese zu vergrößern)
|
Punktwolke |
|
|
|
|
|
Säulendiagramm oder Stabdiagramm |
|
|
siehe auch die Plinko-Demo |
|
|
Größe von Personen
160 | 0 2 2 4 |
Stamm-Blatt-Diagramm Stem-Leaf Plot |
| Pie Chart/Tortendiagramm | |
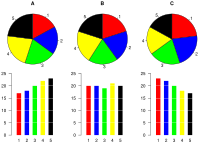
Image via Wikipedia |
Säulendiagramm/Tortendiagramm |
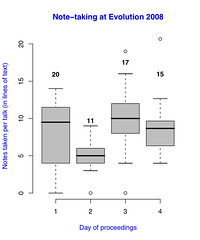
Image by Jeremy B. Yoder via Flickr |
Boxplot |
Vorlesung
In dieser Lektion wird nur die erste Hälfte der Folien benötigt. Der Rest wird in der folgenden Lektion verwendet.
Vorlesungsaufzeichnung
Aufgaben
Der Fragebogen "Einstellung zur Statistik" wurde von 14 Personen beantwortet. Es wurden die folgenden Angaben bezüglich der Merkmale Alter und "Wie lange liegt der Mathematikuntericht zurück" gemacht.
| Nr. | Alter | Jahre seit Matheunterricht |
| 1 | 25 | 5 |
| 2 | 29 | 10 |
| 3 | 21 | 2 |
| 4 | 22 | 3 |
| 5 | 26 | 4 |
| 6 | 27 | 8 |
| 7 | 26 | 9 |
| 8 | 43 | 25 |
| 8 | 23 | 4 |
| 10 | 22 | 3 |
| 11 | 31 | 12 |
| 12 | 22 | 2 |
| 13 | 46 | 27 |
| 14 | 22 | 3 |
Visualisieren Sie die Beobachtungen bei den beiden Merkmalen jeweils als:
- Empirische Verteilungsfunktion
- Säulendiagramm
- Boxplot
- Stamm-Blatt-Diagramm
Welche Darstellung(en) geben die einzelnen Beobachtungen am genauesten wieder?
Lesestoff
 Image via Wikipedia |
Florence Nightingale, Mitglied der Royal Statistical Society |
Lesen Sie den folgenden Beitrag und versuchen Sie zu verstehen, wie die von Florence Nightingale verwendeten Coxcombs zu verwenden sind.

Image by Steve took it via Flickr
tags:
Language:
Lektion 5: Kennzahlen und Darstellungen für unterschiedlich skalierte Merkmale
- Add new comment
- 7276 reads
| Attachment | Size |
|---|---|
| 1019.94 KB |
Übersicht über die Kennzahlen für unterschiedlich skalierte Merkmale:
Vorlesung
Die ersten Folien stammen aus der vorangegangenen Lektion.
Vorlesungsaufzeichnung
tags:
Language:
Quiz: Kennzahlen und Darstellungen für unterschiedlich skalierte Merkmale
- 8867 reads
Wann welche Kennzahl oder welches Diagramm geeignet ist, wird hier gefragt.
Lektion 6: Zentraler Grenzwertsatz und Normalverteilung
- Add new comment
- 20890 reads
| Attachment | Size |
|---|---|
| 97.24 KB |
Zentraler Grenzwertsatz
Der zentrale Grenzwertsatz ist eine wichtige Grundlage für viele theoretische Überlegungen. Er besagt, werden Stichproben aus einer Population in der ein quantitatives Merkmal beliebig verteilt ist gezogen, so ist der Mittelwert des Merkmals in den Stichproben immer annähernd normalverteilt solange ausreichend viele Beobachtungen gemacht werden.
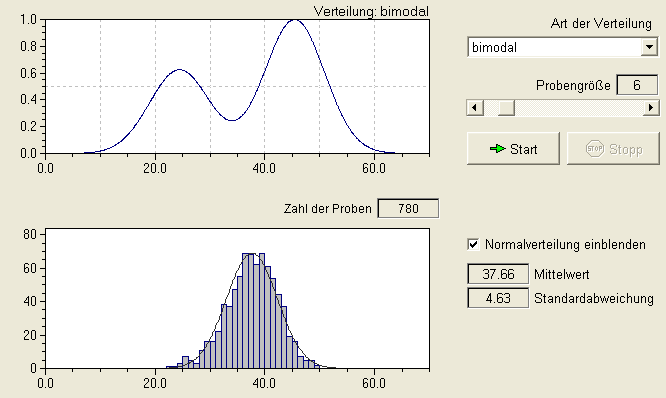
Beispiel: Demoprogramm von Hans Lohninger
Normalverteilung
Lektion Normalverteilung (englisch) aus der Reihe Statistics - An intuitive introduction der University of Nottingham.
Vorlesung
Vorlesungsaufzeichnung
tags:
Language:
Quiz: Zentraler Grenzwertsatz und Normalverteilung
- 9992 reads
Fragen zum zentralen Grenzwertsatz und der Normalverteilung.
Lektion 7: Statistisches Schätzen
- Add new comment
- 10093 reads
| Attachment | Size |
|---|---|
| 381.35 KB | |
| 174.61 KB |
Statistisches Schätzen
- Rechner für Konfidenzintervalle
- Beispiele für Konfidenzintervalle
-
Simulation von Konfidenzintervallen
- Erläuterung 1 zur Simulation von Konfidenzintervallen zur Schätzung des Erwartungswertes einer Verteilung durch das arithm. Mittel einer Stichprobe
-
Erläuterung 2 zur Simulation des Konfidenzintervals zur Schätzung der Erfolgswahrscheinlichkeit durch die relative Häufigkeit des Erfolges in einer Stichprobe
Vorlesung
Aufzeichnung eines Vortrags zu Konfidenzintervallen der KhanAcademy
... und noch ein Beispiel dazu (ebenfalls von der KhanAcademy)
Tabelle "Quantile der t-Verteilung"
Selbsttest
tags:
Language:
Lektion 8: Statistisches Testen
- 8472 reads
| Attachment | Size |
|---|---|
| 558.27 KB |
Statistisches Testen
Vorlesungsaufzeichnung
Vorlesungsaufzeichnung
Selbsttest
... und hier geht's zum Quiz
tags:
Language:
Quiz: Statistisches Testen
- 5169 reads
Überprüfen Sie Ihre Kenntnisse im Bereich "Statistisches Testen". Viel Glück!
Lektion 9: Binomialverteilung
- Add new comment
- 5859 reads
Inhalt kommt noch
f3wyb8em7j
tags:
Language:
Warum brauchen wir Statistik? Ein Beispiel
- Add new comment
- 6209 reads
Im Editorial der New York Times vom 17. März 2009 steht geschrieben:

Estimated HIV/Aids prevalence among young adults (15-49) by country in 2008.
Image via Wikipedia
"As reported on Tuesday by journalists who accompanied the pope on his flight to Africa, Benedict said that distribution of condoms would not resolve the AIDS problem but, on the contrary, would aggravate or increase it. The first half of his statement is clearly right. Condoms alone won’t stop the spread of H.I.V., the virus that causes AIDS. Campaigns to reduce the number of sexual partners, safer-sex practices and other programs are needed to bring the disease to heel.
But the second half of his statement is grievously wrong. There is no evidence that condom use is aggravating the epidemic and considerable evidence that condoms, though no panacea, can be helpful in many circumstances." (Zum Editorial)
Wie sieht nun es mit der letzten Aussage aus? Wie ist der aktuelle Stand des Wissens: Wird die HIV Inzidenz durch die Verwendung von Kondomen beeinflusst? Und falls ja, in welche Richtung?. Hierzu wurde ein systematischer Review der bekannten wissenschaftlichen Literatur im Rahmen der Cochrane Initiative durchgeführt. Das Ergebnis:
"This review indicates that consistent use of condoms results in 80% reduction in HIV incidence. Consistent use is defined as using a condom for all acts of penetrative vaginal intercourse. Because the studies used in this review did not report on the "correctness" of use, namely whether condoms were used correctly and perfectly for each and every act of intercourse, effectiveness and not efficacy is estimated. Also, this estimate refers in general to the male condom and not specifically to the latex condom, since studies also tended not to specify the type of condom that was used. Thus, condom effectiveness is similar to, although lower than, that for contraception." (Zum systematischen Review - Cochrane Library)
Die zweite Aussage des Papstes ist damit zumindest aus wissenschaftlicher Sicht so nicht haltbar. Hier wurde durch die systematische Zusammenfassung methodisch einwandfreier Studien gezeigt, dass die Verwendung von Kondomen die HIV Inzidenz deutlich verringert.
tags:
Language:
Literatur und Medien
- Add new comment
- 5448 reads
Hier finden Sie Hinweise auf Bücher, die in die Statistik einführen.
Zunächst Bücher, die kostenfrei zur Verfügung stehen. Nicht nur in Englisch verfügbar.

Image via Wikipedia
- Wikibook: Statistik (Deutsch/online)
- Electronic Statistic Textbook (English/online)
- UCLA Probability and Statistics Textbook
- Charles M. Grinstead, J Laurie Snell: Introduction to Probability (English/PDF zum Herunterladen)
- Medpage Guide to Biostatistics (English/PDF zum Herunterladen)
(Eher eine Broschüre, bietet aber eine sehr gute Übersicht)
Literaturliste (auch deutschsprachige)
- Meine CiteULike-Liste
Ein vollständiger Kurs (English) ist der Chance Kurs, der versucht, grundlegende Kenntnisse im Umgang mit Zahlen, Mathematik und Statistik zu vermitteln.
- Chance Course
Videos und Lernmaterialien - Vorlesung: Introductory Probability and Statistics for Business, Videoaufzeichnung einer Statistik-Vorlesung. WebCast UC Berkeley
tags:
Language:
Statistik-Software
- 7695 reads
Kommerzielle Statistikpakete bieten einen sehr großen Funktionsumfang, sind aber in der Regel recht teuer, so dass bei einer sehr seltenen Nutzung, etwa anlässlich eines Kurses, überlegt werden muss, ob sich die Investition lohnt. Es gibt aber auch spezielle Ausgaben für Studenten.
Für die kurzfristige Nutzung bieten sich auch kostenfreie Statistkprogramme an. Diese sind meist für einen bestimmten Problembereich entwickelt worden, daher ist der Funktionsumfang oft beschränkt. Auch ist der Bedienungskomfort nicht immer sehr groß. Untenstehend finden Sie zwei umfangreiche Linklisten, die freie Statistikprogramme und Pakete auflisten.
Für Übungen gibt es Rechner für statistische Probleme unter
Für umfangreiche statistische Analysen bietet sich die Sprache R an, die eine sehr gute Open Source Alternative zur kommerziellen Sprache S darstellt.
tags:
Language:
Fragen zur Statistik
- Add new comment
- 41494 reads
Hier können Sie nicht nur Fragen zu den statistischen Verfahren stellen, die in der Veranstaltung behandelt wurden, sondern Sie können auch Antworten zu bestehenden Fragen anbieten. Es ist eine Diskussionsforum, soll also keine Einbahnstraße darstellen, sondern eher der Konversation dienen. Selbstverständlich ist, dass respektvoll miteinander umgegangen wird. Klicken Sie einfach auf Post-Reply oben, um Ihre Frage zu stellen.






![Reblog this post [with Zemanta]](http://img.zemanta.com/reblog_e.png?x-id=b372b96a-fc37-4222-8853-131a72ee8ef0)